目录

• 基本概念
• 二阶方程的特征理论和分类
• 分离变量法
• 双曲型方程
• 抛物型方程
• 椭圆形方程

基本概念

偏微分方程

关于多元未知函数$u\left(x_{1}, \cdots, x_{n}\right)$及其偏导数的关系式：
$$F\left(x_{1}, \cdots, x_{n}, u, D u, D^{2} u, \cdots, D^{m} u\right)=0$$

1. 偏微分方程的阶数：未知函数偏导数最高阶数。
2. 线性偏微分方程：未知函数和未知函数的各阶偏导都是线性的。
   $$\sum_{|\alpha| \leq m} c_{\alpha}(x) D^{\alpha} u=f(x)$$
   • 其中$c_{\alpha}(x)(|\alpha| \leq m)$和$f \left ( x \right )$都是不依赖于$u$和它的各阶偏导。
   • 自由项：线性偏微分方程中不含$u$及其偏导数的项。
   • 齐次方程：自由项为0
3. 非线性偏微分方程
   • 拟线性偏微分方程：在非线性偏微分方程中，关于未知函数的所有最高阶偏导数都是线性的。
     $$\sum_{|\alpha|=m} c_{\alpha}\left(D^{m-1} u, \cdots, D u, u, x\right) D^{\alpha} u+c\left(D^{m-1} u, \cdots, D u, u, x\right)=0$$
   • 主部：在拟线性偏微分方程中，由最高阶偏导数组成的部分。
   • 半线性：主部的系数都是常数或是自变量的已知函数.
     $$\sum_{|\alpha|=m} c_{\alpha}(x) D^{\alpha} u+c\left(D^{m-1} u, \cdots, D u, u, x\right)=0$$

经典方程

我们这门课程主要讲的就是三类基本方程。

1. 弦振动方程。
2. 热传导方程。
3. Laplace方程。

定解问题

1. 泛定方程：描绘普通规律的方程称为泛定方程。
2. 定解条件：初始条件（Cauchy问题）和边界条件
3. 三类典型边界条件：
   • 第一边界问题（Dirichlet问题）
     $$\left.u\right|_{\Gamma}=\varphi(x, y, z, t)$$
   • 第二边界问题（Neumann问题）
     $$\left.\frac{\partial u}{\partial v}\right|_{\Gamma}=\varphi(x, y, z, t)$$
   • 第三边界问题（Robin问题）
     $$\left.\left(\frac{\partial u}{\partial v}+\sigma u\right)\right|_{\Gamma}=\varphi(x, y, z, t)$$
4. 适定性：满足下面三个条件的定解问题，称为适定的。
   • 存在性：至少存在一个解
   • 唯一性：至多存在一个解
   • 稳定性：定解条件微小变动的情况下，解也只做微小变动。

二阶方程的特征理论和分类

二阶方程的特征

考虑一般的二阶线性方程：
$$\sum_{i, j=1}^{n} a_{i j} \frac{\partial^{2} u}{\partial x_{i} \partial x_{j}}+\sum_{i=1}^{n} b_{i} \frac{\partial u}{\partial x_{i}}+c u=f$$
其中$a_{ij}$, $b_i$, $c$, $f$ 为$x_{1}, \cdots, x_{n}$的已知函数，且在$R^n$内连续可微，$a_{ij} = a_{ji}$.

特征曲面和特征方程

假设$S$是R^n空间的一个曲面。
$$S: G\left(x_{1}, x_{2}, \cdots, x_{n}\right)=0$$
若：
$$\sum_{i, j=1}^{n} a_{i j} \frac{\partial G}{\partial x_{i}} \frac{\partial G}{\partial x_{j}}=0$$
称$S$为特征曲面。

称：
$$\sum_{i, j=1}^{n} a_{i j} \alpha_{i} \alpha_{j}=0$$
为偏微分方程的特征方程。

特征方程在点$P\left(x_{1}^{0}, \cdots, x_{n}^{0}\right)$处的解$l\left(\alpha_{1}, \cdots, \alpha_{n}\right)$为偏微分方程在点$P$处的特征方向。

两个自变量的情形

两个自变量的二阶拟线性偏微分方程的一般形式
$$a u_{x x}+2 b u_{x y}+c u_{y y}=F$$
假设$\Gamma$是平面$xoy$上的一条曲线。
当$\Gamma: x=\varphi(t), \quad y=\psi(t)$时，若
$$\Delta=a \psi^{\prime 2}-2 b \varphi^{\prime} \psi^{\prime}+c \varphi^{\prime 2} = 0$$

• $b$前面为什么是负号：看笔记，是根据一个三元$(U_{xx}, U_{xy}, U_{yy})$线性方程组行列式为0得出的特征方程。

称$\Gamma$为特征曲线。
$$a \mathrm{d} y^{2}-2 b \mathrm{d} x \mathrm{d} y+c \mathrm{d} x^{2}=0$$
为偏微分方程的特征方程。

当$\Gamma: y=\psi(x)$时$(a \neq 0)$，有
$$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{b \pm \sqrt{b^{2}-a c}}{a}$$

当$\Gamma: \varphi(x, y)=0$时，特征方程为
$$a \varphi_{x}^{2}+2 b \varphi_{x} \varphi_{y}+c \varphi_{y}^{2}=0$$
这是因为
$$\varphi_{x} dx + \varphi_{y} dy=0$$
对$\Gamma: \varphi(x, y)=0$两边微分的结果。这与多个自变量的情形的定义是一致的。

二阶方程的分类

两个自变量的情形

考虑以下线性偏微分方程
$$a u_{x x}+2 b u_{x y}+c u_{y y}+d u_{x}+e u_{y}+g u=f$$
其中$a, b, c, d, e, g, f 是x,y$的已知函数。

做变量变换
$$\left{\begin{array}{l}
\xi=\varphi(x, y) \
\eta=\psi(x, y)
\end{array}\right.$$
方程可转换为
$$A \frac{\partial^{2} u}{\partial \xi^{2}}+2 B \frac{\partial^{2} u}{\partial \xi \partial \eta}+C \frac{\partial^{2} u}{\partial \eta^{2}}+D \frac{\partial u}{\partial \xi}+E \frac{\partial u}{\partial \eta}+G u=F$$
二阶偏导
$$\begin{array}{c}
\frac{\partial^{2} u}{\partial x^{2}}=\frac{\partial^{2} u}{\partial \xi^{2}}\left(\frac{\partial \xi}{\partial x}\right)^{2}+2 \frac{\partial^{2} u}{\partial x} \frac{\partial \eta}{\partial x}+\frac{\partial^{2} u}{\partial n^{2}}\left(\frac{\partial \eta}{\partial x}\right)^{2}+\frac{\partial^{2} \xi}{\partial x^{2}}+\frac{\partial^{2} \eta}{\partial x^{2}} \
\frac{\partial^{2} u}{\partial x \partial y}=\frac{\partial^{2}}{\partial \varepsilon^{2}} \frac{\partial \xi}{\partial x} \frac{\partial \xi}{\partial y}+\frac{\partial^{2} u}{\partial \xi \partial n}\left(\frac{\partial \xi}{\partial x} \frac{\partial \eta}{\partial y}+\frac{\partial \xi}{\partial y} \frac{\partial \eta}{\partial x}\right)+\frac{\partial^{2}}{\partial x^{2}} \frac{\partial \eta}{\partial x} \frac{\partial \eta}{\partial y}+\frac{\partial u}{\partial x \partial y}+\frac{\partial^{2} \xi}{\partial x \partial y} \
\frac{\partial^{2} u}{\partial y^{2}}=\frac{\partial^{2} u}{\partial \xi^{2}}\left(\frac{\partial \xi}{\partial y}\right)^{2}+2 \frac{\partial^{2} \eta}{\partial \xi(\eta)} \frac{\partial \xi}{\partial y} \frac{\partial \eta}{\partial y}+\frac{\partial^{2} u}{\partial n^{2}}\left(\frac{\partial \eta}{\partial y}\right)^{2}+\frac{\partial^{2} \xi}{\partial y^{2}}+\frac{\partial^{2} \eta}{\partial y^{2}}
\end{array}$$
带入可得
$$\left{\begin{array}{l}
A(\xi, \eta)=a \varphi_{x}^{2}+2 b \varphi_{x} \varphi_{y}+c \varphi_{y}^{2} \
B(\xi, \eta)=a \varphi_{x} \psi_{x}+b\left(\varphi_{x} \psi_{y}+\varphi_{y} \psi_{x}\right)+c \varphi_{y} \psi_{y} \
C(\xi, \eta)=a \psi_{x}^{2}+2 b \psi_{x} \psi_{y}+c \psi_{y}^{2} \
D(\xi, \eta)=a \varphi_{x x}+2 b \varphi_{x y}+c \varphi_{y y}+d \varphi_{x}+e \varphi_{y} \
E(\xi, \eta)=a \psi_{x x}+2 b \psi_{x y}+c \psi_{y y}+d \psi_{x}+e \psi_{y} \
G(\xi, \eta)=g(x, y) \
F(\xi, \eta)=f(x, y)
\end{array}\right.$$
最后的A到G还需要通过变换
$$\left{\begin{array}{l}
\xi=\varphi(x, y) \
\eta=\psi(x, y)
\end{array}\right.$$
将$(x,y)$成$(\xi, \eta)。$

一个记忆法，把A-E写成矩阵形式。（笔记）

方程判别式
$$\Delta=b^{2}-a c$$
$$\Delta^{\prime}=B^{2}-A C$$
他们之间有着如下的关系
$$\Delta^{\prime}=J^{2} \Delta$$
$$J=\left|\begin{array}{ll}
\varphi_{x} & \varphi_{y} \
\psi_{x} & \psi_{y}
\end{array}\right|$$

在$J \neq 0$的情况下，$\Delta = \Delta^{\prime}$，所以这是可逆自变换下的不变性。通过这个来分类。
$$\begin{array}{l}
\Delta>0 双曲型偏微分方程\
\Delta=0 抛物型偏微分方程\
\Delta<0 椭圆形偏微分方程
\end{array}$$

方程标准型

考虑两个自变量常系数的情形：
$$a u_{x x}+2 b u_{x y}+c u_{y y}+d u_{x}+e u_{y}+g u=f(x, y)$$
其中$a, b, c, d,e,g$都是常数。

情形1： 双曲型方程的标准型 $\Delta > 0$

两族实特征线为：
$$\left{\begin{array}{l}
y-\frac{b+\sqrt{\Delta}}{a} x=c_{1} \
y-\frac{b-\sqrt{\Delta}}{a} x=c_{2}
\end{array}\right.$$
做变换
$$ \left{\begin{array}{l}
\xi =y-\frac{b+\sqrt{\Delta}}{a} \
\eta = y-\frac{b-\sqrt{\Delta}}{a} x
\end{array}\right.$$
方程化为双曲型方程的第一标准型(只含混合导数)
$$ u_{\xi \eta} = Du_{\xi} + Eu_\eta +Gu+F(\xi, \eta)$$
引入变换
$$\bar{x}=\xi+\eta, \quad \bar{y}=\xi-\eta$$
方程可化为双曲型方程的第二标准型(不含混合导数)
$$u_{\bar{x}\bar{x}}-u_{\bar{y} \bar{y}}=D_{1} u_{\bar{x}}+E_{1} u_{\bar{y}}+G_{1} u+F_{1}(\bar{x}, \bar{y})$$

情形2： 抛物型方程的标准型 $\Delta = 0$

只有一族实特征线：
$$ y - \frac{b}{a}x = c$$
引入变换
$$ \xi = y- \frac{b}{a}x, \eta = y$$
方程化为抛物型方程的标准型(只剩下$\eta$的二阶偏导)
$$ u_{\eta \eta} = Du_{\xi} + Eu_\eta +Gu+F(\xi, \eta)$$

情形3： 抛物型方程的标准型 $\Delta > 0$

做变换：
$$ \left{\begin{array}{l}
\xi =y-\frac{b+i\sqrt{\Delta}}{a} \
\eta = y-\frac{b-i\sqrt{\Delta}}{a} x
\end{array}\right.$$
再作变换抽取出实部和虚部
$$\left{\begin{array}{l}\bar{\xi}=\frac{1}{2}(\xi+\eta)=y-\frac{b}{a} x \ \bar{\eta}=\frac{1}{2 i}(\xi-\eta)=-\frac{\sqrt{a c-b^{2}}}{a} x\end{array}\right.$$
方程化为椭圆型方程的标准型
$$ u_{\bar\eta \bar\eta} + u_{\bar\xi \bar\xi} = Du_{\xi} + Eu_\eta +Gu+F(\bar\xi, \bar\eta)$$

变系数

变系数需要根据系数判断$\Delta$的正负（有可能区域不同有不同类型的标准型），对特征方程进行积分，再做适当的特征变换。

多变量的分类与标准型

只考虑主部为常系数的情形
$$\sum_{i, j=1}^{n} a_{i j} \frac{\partial^{2} u}{\partial x_{i} \partial x_{j}}+\sum_{i=1}^{n} b_{i}\left(x_{1}, \cdots, x_{n}\right) \frac{\partial u}{\partial x_{i}}+c\left(x_{1}, \cdots, x_{n}\right) u=f\left(x_{1}, \cdots, x_{n}\right)$$
其中$a_{ij} = a_{ji}$，上式的特征方程为
$$\sum_{i, j=1}^{n} a_{i j} \alpha_{i} \alpha_{j}=0$$
记$D = \sum_{i, j=1}^{n} a_{i j} \alpha_{i} \alpha_{j}$为方程的特征二次型。
存在可逆线性变换
$$\left(\begin{array}{c}\alpha_{1} \ \alpha_{2} \ \vdots \ \alpha_{n}\end{array}\right)=B\left(\begin{array}{c}\beta_{1} \ \beta_{2} \ \vdots \ \beta_{n}\end{array}\right)$$
使得特征二次型化为标准型
$$D = \sum_{i, j=1}^{n} \lambda_{i} \beta_{i}^2$$
其中$\lambda_i = 0, -1, 或1$.
对自变量做变换
$$\left(\begin{array}{c}y_{1} \ y_{2} \ \vdots \ y_{n}\end{array}\right)=B^{T}\left(\begin{array}{c}x_{1} \ x_{2} \ \vdots \ x_{n}\end{array}\right)$$
就可以将偏微分方程化为
$$\sum_{i=1}^{n} \lambda_{i} \frac{\partial^{2} u}{\partial y_{i}^{2}}+\sum_{i=1}^{n} B_{i}\left(y_{1}, \cdots, y_{n}\right) \frac{\partial u}{\partial y_{i}}+C\left(y_{1}, \cdots, y_{n}\right) u=F\left(y_{1}, \cdots, y_{n}\right)$$

多变量分类

1. $\lambda_i$全是1，椭圆型方程。
2. 其中一个是1，其余负1.或者其中一个负1，其余都是1.双曲型。
3. 一个是0，其余全是1或全是负1.抛物型。

分离变量法

解题步骤

分离变量法的解题步骤可分为三步。

1. 第一步：令$u(x,t) - X(x)T(t)$代入方程和边界条件。从而定出$X(x)$所适合的Sturm-Lioubille 问题及$T(t)$适合的常微分方程。
2. 第二步：解Sturm-Liouville问题，求出全部特征值和特征函数, 并求出相应的$T(t)$的表达式.
3. 第三步：将所有变量分离形式的特解叠加起来，并利用初始条件定出所有待定常数

具体操作通过具体案例来体现。看笔记。

求解实例

课本P40

双曲型方程

Duhamel原理

非常有用的一个原理，将非齐次方程定解问题的求解转为齐次方程定解问题的求解。除了双曲型方程，抛物型方程也适用。

考虑在$\mathbb{R}^{n} \times[0, \infty)$上的$n$维波动方程。

$$\left{\begin{array}{ll}\square u=\frac{\partial^{2} u}{\partial t^{2}}-a^{2} \Delta u=f\left(x_{1}, \cdots, x_{n}, t\right), & \left(x_{1}, \cdots, x_{n}, t\right) \in \mathbb{R}^{n} \times(0, \infty) \ u\left(x_{1}, \cdots, x_{n}, 0\right)=\varphi\left(x_{1}, \cdots, x_{n}\right), & \left(x_{1}, \cdots, x_{n}\right) \in \mathbb{R}^{n} \ u_{t}\left(x_{1}, \cdots, x_{n}, 0\right)=\psi\left(x_{1}, \cdots, x_{n}\right), & \left(x_{1}, \cdots, x_{n}\right) \in \mathbb{R}^{n}\end{array}\right.$$
因为方程是线性的
可以将方程拆成下述三个定解问题。
$$(\mathrm{I})\left{\begin{array}{l}\square u_{1}=0 \ u_{1}\left(x_{1}, \cdots, x_{n}, 0\right)=\varphi\left(x_{1}, \cdots, x_{n}\right) \ u_{1 t}\left(x_{1}, \cdots, x_{n}, 0\right)=0\end{array}\right.$$

$$(\mathrm{II})\left{\begin{array}{l}\square u_{1}=0 \ u_{1}\left(x_{1}, \cdots, x_{n}, 0\right)=0 \ u_{1 t}\left(x_{1}, \cdots, x_{n}, 0\right)=\psi\left(x_{1}, \cdots, x_{n}\right)\end{array}\right.$$

$$(\mathrm{III})\left{\begin{array}{l}\square u_{1}=f\left(x_{1}, \cdots, x_{n}, t\right) \ u_{1}\left(x_{1}, \cdots, x_{n}, 0\right)=0 \ u_{1 t}\left(x_{1}, \cdots, x_{n}, 0\right)=0\end{array}\right.$$

接下来，首先要的解的是问题$\mathrm{II}$。(分离变量还有其他吗？)

设$u_2 = U_{\psi}\left(x_{1}, \cdots, x_{n}, t\right)$是$\mathrm{II}$的解，则$\mathrm{I}$，$\mathrm{III}$的解$u_1, u_3$可分别表示为：

$$u_{1}\left(x_{1}, \cdots, x_{n}, t\right)=\frac{\partial}{\partial t} U_{\varphi}\left(x_{1}, \cdots, x_{n}, t\right)$$

$$u_{3}\left(x_{1}, \cdots, x_{n}, t\right)=\int_{0}^{t} U_{f_{\tau}}\left(x_{1}, \cdots, x_{n}, t-\tau\right) \mathrm{d} \tau$$

这里的$U_{\psi}，U_{\varphi}，U_{f_{\tau}}$表示当$\mathrm{II}$里的$U_{\psi}$用$U_{\varphi}$或者$U_{f_{\tau}}$换掉后的解。

混合问题

1. 边界条件齐次化。通过线性函数将边界条件化为0.
   $$U(x, t)=\mu_{1}(t)+\frac{x}{l}\left(\mu_{2}(t)-\mu_{1}(t)\right)$$
   $$U(x, t)=x\mu_{1}(t)+\frac{x^2}{2l}\left(\mu_{2}(t)-\mu_{1}(t)\right)$$

一维波动方程

齐次波动方程的Cauchy问题和特征线法。

定解问题如下
$$u_{t t}-a^{2} u_{x x}=0, \quad-\infty<x<\infty, \quad t>0$$
$$u(x, 0)=\varphi(x), \quad u_{t}(x, 0)=\psi(x), \quad-\infty<x<\infty$$
特征线解法见笔记。

D’Alembert公式

通过对齐次波动方程的Cauchy问题用特征线法导出的D’Alembert公式
$$u(x, t)=\frac{1}{2}[\varphi(x-a t)+\varphi(x+a t)]+\frac{1}{2 a} \int_{x-a t}^{x+a t} \psi(\tau) \mathrm{d} \tau$$
D’Alembert公式不仅给出了弦振动方程柯西问题解的表达式, 还可用于求解四分之一平面上的问题以及导出弦振动方程的一些重要性质.

依赖区域、决定区域和影响区域

• 依赖区域：
  
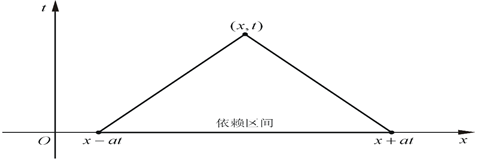
  依赖区域是指上述的解$u(x,t)$在点$(x,t)$依赖于数值依赖于这一片区域。
  $$[x-at, x+at]$$
• 决定区域：
  
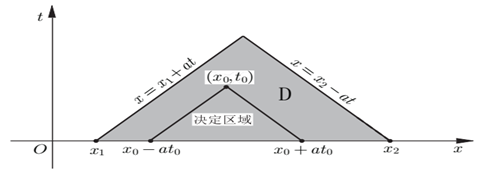
  决定区域是指给定$[x_1, x_2]$，能决定$xOt$上那些点的函数值。
  $$D: {(x,t) |x_1 + at \leq x \leq x_2 - at,\ \ t>0}$$
• 影响区域
  
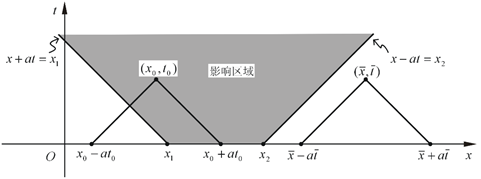
  影响区域是指给定$[x_1, x_2]$，会影响到$xOt$上那些点的函数值。
  $$G: {(x,t) |x_1 - at \leq x \leq x_2 + at,\ \ t>0}$$

高维波动方程

考虑三维齐次波动方程的Cauchy问题，
$$\left{\begin{array}{l}u_{t t}-a^{2}\left(u_{x x}+u_{y y}+u_{z z}\right)=0,-\infty<x, y, z<\infty, t>0 \ \left.u\right|{t=0}=\varphi(x, y, z),\left.u{t}\right|{t=0}=\psi(x, y, z),-\infty<x, y, z<\infty\end{array}\right.$$
根据一维D’Alembert猜测高维的D’Alembert公式也具有下述形式的解。称为Poisson公式。
$$u(x, y, z, t)=\frac{\partial}{\partial t}\left(t v{\varphi}(x, y, z, t)\right)+t v_{\psi}(x, y, z, t)$$
其中
$$\left{\begin{array}{l}v_{\varphi}(x, y, z, t)=\frac{1}{4 \pi a^{2} t^{2}} \iint_{S_{a t}(M)} \varphi \mathrm{d} S \ v_{\psi}(x, y, z, t)=\frac{1}{4 \pi a^{2} t^{2}} \iint_{S_{a t}(M)} \psi \mathrm{d} S\end{array}\right.$$
$\frac{1}{4 \pi a^{2} t^{2}}$是$at$为半径的球面上的平均值。

对于偶数维的，采用降维法，补充一个变量变成高一维的奇数维求解。

高维依赖区域

变成了圆锥。

小结

抛物型方程

热传导方程定解问题的求解

齐次热方程的Cauchy问题

方程如下：
$$\left{\begin{array}{ll}u_{t}-a^{2} u_{x x}=0, & -\infty<x<\infty, t>0 \ \left.u\right|{t=0}=\varphi(x), & -\infty<x<\infty\end{array}\right.$$
要背：解的表达式——Poisson公式：
$$u(x, t)=\int{-\infty}^{\infty} G(x-y, t) \varphi(y) \mathrm{d} y$$
其中热核函数：
$$G(x, t)=\left{\begin{array}{ll}\frac{1}{2 a \sqrt{\pi t}} \mathrm{e}^{-\frac{x^{2}}{4 a^{2} t}}, & t>0 \ 0, & t<0\end{array}\right.$$

非齐次热方程的Cauchy问题

方程如下：
$$\left{\begin{array}{ll}u_{t}-a^{2} u_{x x}=f(x,t), & -\infty<x<\infty, t>0 \ \left.u\right|{t=0}=\varphi(x), & -\infty<x<\infty\end{array}\right.$$
要背：解的表达式：
$$u(x, t)=\int{-\infty}^{\infty} G(x-y, t) \varphi(y) \mathrm{d} y+\int_{0}^{t} \int_{-\infty}^{\infty} G(x-y, t-\tau) f(y, \tau) \mathrm{d} y \mathrm{d} \tau$$
其中热核函数：
$$G(x, t)=\left{\begin{array}{ll}\frac{1}{2 a \sqrt{\pi t}} \mathrm{e}^{-\frac{x^{2}}{4 a^{2} t}}, & t>0 \ 0, & t<0\end{array}\right.$$

半直线上的混合问题

$$\left{\begin{array}{ll}u_{t}-a^{2} u_{x x}=f(x, t), & 0<x<\infty, t>0 \ u(x, 0)=\varphi(x), & 0 \leq x<\infty \ u(0, t)=\mu(t), & t \geq 0\end{array}\right.$$
先将边界条件齐次化：$v(x,t) = u(x,t) - \mu (x,t)$
就有：
$$\left{\begin{array}{l}v_{t}-a^{2} v_{x x}=f(x, t)-\mu^{\prime}(t) \ \left.v\right|{t=0}=\varphi(x)-\mu(0) \ \left.v\right|{x=0}=0\end{array}\right.$$
在由叠加原理，分成两个问题。结合奇延拓法求解。

热核函数常见变换

1. $\mathrm{e}^{-\frac{(x-y)^{2}}{4 a^{2} t}}$，做$z=\frac{x-y}{2a \sqrt t}$

   就会变成：
   $$\begin{aligned} I_{1} &=\frac{1}{2 a \sqrt{\pi t}} \int_{-\infty}^{0} A \mathrm{e}^{-\frac{(x-y)^{2}}{4 a^{2} t}} \mathrm{d} y \ &=-\frac{A}{\sqrt{\pi}} \int_{+\infty}^{\frac{x}{2 a \sqrt{t}}} \mathrm{e}^{-z^{2}} \mathrm{d} z \end{aligned}$$
   最后，记：
   $$\operatorname{erf}(s)=\frac{2}{\sqrt{\pi}} \int_{0}^{s} \mathrm{e}^{-z^{2}} \mathrm{d} z, \quad \operatorname{erf}(s)=1-\operatorname{erf}(s)$$

2. $$\frac{1}{\sqrt \pi}\int_{-\infty}^{\infty}e^{-x^2}dx = 1$$

3. $$\int_{0}^{+\infty} e^{-x^{2}} \cos r x d x=\frac{\sqrt{\pi}}{2} e^{-\frac{r^{2}}{4}}$$

极值原理

弱极值原理

$f(x,t)\leq0$且$u \in C^{2,\ 1}(Q_T) \cap C(\bar{Q_T})$的解则$u(x,t)$的最大值必定在$Q_T$的抛物边界$\Gamma_T$上达到.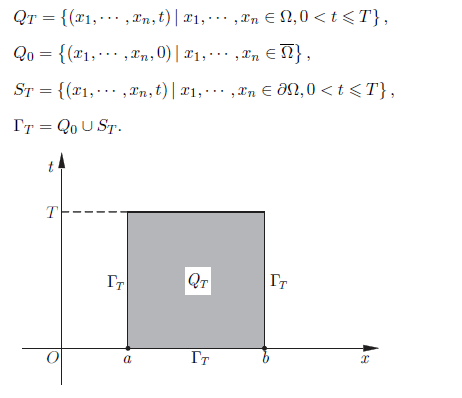

证明用反证法。
构造：
$$v(x, t)=u(x, t)+\frac{M-m}{4 n d^{2}}\left|x-x^{*}\right|^{2}, \quad$$
其中
$$d=\max {|x-y| \mid x, y \in \bar{\Omega}}$$
然后用强极值原理

一般情况下的弱极值原理

$$L u=u_{t}-a^{2} \Delta u+\sum_{i}^{n} b_{i}(x, t) u_{x_{i}}+c(x, t) u=f(x, t)$$
设$c(x,t) \geq 0, f(x,t)\leq0$，$u \in C^{2,\ 1}(Q_T) \cap C(\bar{Q_T})$

则$u(x,t)$在$\bar Q$上非负最大值(如果存在的话) 必在$\Gamma$上达到。

定理

上述若$c(x,t)\geq -c_0$，如果 $\max {\Gamma{T}} u(x, t) \leqslant 0,$ 那么必有 $\max {\bar{Q}{T}} u(x, t) \leqslant 0$

反证法：令$v(x,t) = e^{-c_0t}u(x,t)$

比较原理

$$\mathcal{L} u=u_{t}-a^{2} \Delta u+\sum_{i}^{n} b_{i}(x, t) u_{x_{i}}+c(x, t) u=f(x, t)$$
$c(x,t)\geq -c_0$且$u,\ v \in C^{2,\ 1}(Q_T) \cap C(\bar{Q_T})$的解，$\mathcal{L} u \leqslant \mathcal{L} v$，$\left.u\right|{\Gamma{T}} \leqslant\left. v\right|{\Gamma{T}},$ 则在 $\bar{Q}_{T}$ 上: $u(x, t) \leqslant v(x, t)$

应用

这个是个特殊些的例子

先做齐次变换，再构造$W = Ft+B$，其中
$F = max_{\bar Q_T}|f_t(x,t)|$，$B = $max|\phi(x)|$
最后用比较原理。

另一个比较特殊的应用例子


凸函数，存在$\alpha$，使得
$$ f(u_x) \geq f(v_x) + \alpha (u_x - v_x)$$

还有这种，需要先求导

再通过函数变换, 归结为极值原理的应用.

两类方程的对比

波动方程

$$\left{\begin{array}{l}u_{t t}-a^{2} u_{x x}=f(x, t), \quad x \in \mathbb{R}^{1}, t>0 \ \left.u\right|{t=0}=\varphi(x),\left.u{t}\right|{t=0}=\psi(x), \quad x \in \mathbb{R}^{1}\end{array}\right.$$
解的表达式
$$\begin{aligned} u(x, t)=& \frac{1}{2}[\varphi(x-a t)+\varphi(x+a t)]+\frac{1}{2 a} \int{x-a t}^{x+a t} \psi(\tau) \mathrm{d} \tau \ &+\frac{1}{2 a} \int_{0}^{t} \int_{x-a(t-t)}^{x+a(t-t)} f(\xi, \tau) \mathrm{d} \xi \mathrm{d} \tau \end{aligned}$$

热方程

$$\left{\begin{array}{l}u_{t}-a^{2} u_{x x}=f(x, t), \quad x \in \mathbb{R}^{1}, t>0 \ \left.u\right|{t=0}=\varphi(x), \quad x \in \mathbb{R}^{1}\end{array}\right.$$
解的表达式：
$$u(x, t)=\int{-\infty}^{\infty} G(x-y, t) \varphi(y) \mathrm{d} y+\int_{0}^{t} \int_{-\infty}^{\infty} G(x-y, t-\tau) f(y, \tau) \mathrm{d} y \mathrm{d} \tau$$

光滑性对比

1. 波动方程光滑性与初始数据的光滑性相同。$u \in C^{2}
2. 热方程的解具有很好的光滑性，$u \in C^{\infty}$

决定区域和影响区域对比

1. 波动方程，是斜率为$\alpha$的特征锥内部。
2. 热方程影响区域是整个上半平面，扰动传播速度无限。

极值原理

1. 热传导方程存在极值原理, 而波动方程没有极值原理.

椭圆形方程

调和函数

定义：在有界趋于$\Omega \in R^n$内有直到二阶的连续偏导数, 且在$\Omega$内满足$\Delta_nu=0$，则有基本解。
$$u(r)=\left{\begin{array}{ll}\ln \frac{1}{r}, & n=2 \ \frac{1}{r^{n-2}}, & n \geq 3\end{array}\right.$$

极坐标

对二维的Laplace算子, 在极坐标
$$ x = x_0 + r \cos \theta,\quad y = y_0 + r \sin \theta$$
变换下，有：
$$\Delta_{2} u=\frac{\partial^{2} u}{\partial r^{2}}+\frac{1}{r} \frac{\partial u}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2} u}{\partial \theta^{2}}$$

Green公式

散度定理

设$\Omega$时$n$维空间中足够光滑的曲面$\Gamma$所围成的有界连通区域。$v$是曲面的单位外法向量。若函数$P_i(x_1,\dots, x_n),(i=1,\dots,n)$在闭区域$\Omega + \Gamma$上连续，在$\Omega$上有一阶连续偏导。则：
$$\int_{\Omega} \sum_{i=1}^{n} \frac{\partial P_{i}}{\partial x_{i}} \mathrm{d} x_{1} \cdots \mathrm{d} x_{n}=\int_{\Gamma} \sum_{i=1}^{n} P_{i} \cos \left(\nu, x_{i}\right) \mathrm{d} S$$

由散度定理推第一，第二Green公式。
$u,v$有二阶连续偏导。令
$$P_{i}=u \frac{\partial v}{\partial x_{i}}, \quad i=1,2, \cdots, n$$
就有
$$\int \cdots \int_{\Omega} \sum_{i=1}^{n} \frac{\partial}{\partial x_{i}}\left(u \frac{\partial v}{\partial x_{i}}\right) \mathrm{d} x_{1} \cdots \mathrm{d} x_{n}=\int \cdots \int_{\Gamma} u \sum_{i=1}^{n} \frac{\partial v}{\partial x_{i}} \cos \left(\nu, x_{i}\right) \mathrm{d} S$$
可以用Laplace算子改写为
$$\int \cdots \int_{\Omega} u \Delta_{n} v \mathrm{d} \Omega+\int \cdots \int_{\Omega} \sum_{i=1}^{n} u_{x_{i}} v_{x_{i}} \mathrm{d} \Omega=\int \cdots \int_{\Gamma} u \frac{\partial v}{\partial \nu} \mathrm{d} S$$

第一Green公式
$$\int_{\Omega} v \Delta_n u d x=\int_{\partial \Omega} v \frac{\partial u}{\partial \vec{n}} \mathrm{d} S-\int_{\Omega} \nabla u \cdot \nabla v \mathrm{d} x$$
将$u,v$换位置，相减。
第二Green公式
$$\int_{\Omega}(u \Delta_n v-v \Delta_n u) \mathrm{d} \Omega=\int_{\partial \Omega}\left(u \frac{\partial v}{\partial n}-v \frac{\partial u}{\partial n}\right) \mathrm{d} S$$

调和函数的平均值公式

调和函数在其定义域 Ω 内任一点的值等于它在以该点为心且包含于 Ω 的球面（球体）上的平均值:
$$u(x)=\frac{1}{\left|\partial B_{R}(x)\right|} \int_{\alpha_{R}(x)} u \mathrm{d} S_{\xi}, \quad B_{R}(x) \subset \Omega$$
$$u(x)=\frac{1}{\left|B_{R}(x)\right|} \int_{B_{R}(x)} u(\xi) \mathrm{d} \xi, \quad B_{R}(x) \subset \Omega$$
可以用来计算$u$在某一点的值。

赏

谢谢老板

支付宝

微信